 本站提倡有节制游戏,合理安排游戏时间,注意劳逸结合。
本站提倡有节制游戏,合理安排游戏时间,注意劳逸结合。 <i id='56E2F16849'><strike id='56E2F16849'><tt id='56E2F16849'><pre id='56E2F16849'></pre></tt></strike></i> 常用的食品生物素污一级模型主要有Logistic方程、Gomp-ertz模型、中微展Baranyi&Roberts模型、菌毒究进Bohzmann模型、染预致死模型。测模

Y=a·exp[-exp(b-cx)]
式中两个模型中的型研参数只是数学意义上的参数(a,b,粮油c,食品生物素污…),中微展并不具有生物学意义,菌毒究进不能直接用于微生物生长曲线的染预拟合。需要对其中的测模参数进行修改,使用具有生物学意义的型研参数如(λ,μm,粮油A)来代替纯数学参数(a,b,c,…)。
修正后的Logistic模型:
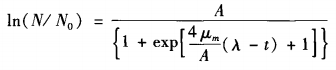
修正后的Gompertz模型:

式中:μm为最大比生长速率,定义为生长曲线拐点处的斜率;λ为迟滞期时间,滞后期被定义为定义最大特定生长速率的线与时间轴的交点;t为培养时间;A指微生物数量达最大值;N0为初始孢子数;N为t时间后存活的孢子数量。Dantigny等通过实验比较Logistic模型和Gompertz模型,通过比较RMSE值(均方根误差)发现两者拟合优度类似,无法确定哪种模型在特定实验条件下为首选,继而通过评估其他标准如参数估计值的准确性来进一步判断如:评估孢子萌发时间(50%孢子萌发所需时间)时,L0-gistic模型的精确度更高;而Gompertz模型可以更准确地估计迟滞期时间。



式中:μm为最大比生长速率(定义为拐点处生长曲线的斜率)(mm/d,μm/h);λ为迟滞期时间;t为培养时间;A为微生物数量最大值。
Lo’pez等评估微生物生长模型(光密度方法定量)确定包括真菌和细菌在内物种,采用包括
Gompertz和Baranyi&Roberts模型在内的各种模型进行拟合,发现Baranyi&Roberts模型拟合度最高;Matin等研究lineal模型、Gompertz模型及Baranyi&Roberts模型对14种常见食物腐败真菌生长一级模型的适用性,采用菌落直径进行生长速率表征发现:当所获数据没有发现渐进趋势时,使用liner模型和Baranyi&Roberts模型可以更好地估计最大生长速率和迟滞期;当观察到生长速率随时问降低时,Baranyi&Roberts模型的拟合度更高。
模拟温度高低或致死剂浓度对微生物群体致死处理模型时,使用经典的一级方程对孢子灭活建立模型:

式中:N为孢子数;N0为初始孢子数;N(t)为经过处理后孢子数;ki为致死率/min-1。
现今大多数孢子灭活模型研究采用线性灭活方法,但是目前对于孢子灭活的研究还较少且只有少部分应用于真菌。
二级模型主要有Ratkowsky平方根模型、Arrhenius-Davey模型、Rosso cardinal模型、Polynomia模型、Gamma Concept模型。
该模型最初是为细菌开发的。

式中:μm为最大比生长速率;b2、C2均为假定系数;Tmin2,为最低生长温度;Tmin2为最高生长温度。通常该模型仅有温度变量,Tassou等刊在建立温度和水分活度对合成葡萄汁培养基上希腊酿酒葡萄中2种产生赭曲霉A的炭曲霉菌株模型时,将Ratkowsky平方根模型变量拓展到其他变量因素上如水分活度。
最初用于描述温度对细菌生长的影响,Panagou等副模拟温度、pH和水分活度对从绿茶橄榄提取的红曲霉生长速度影响时,将该模型变量因素延伸到pH和水分活度。
1nμmax=C0+C1/T+C2/T2
式中:μ为菌落生长速率;T为开氏温度;C0、C1、C2为3个参数。
Rosso等在1993年提出了这个温度模型,使用3个基本温度(Tmin、Tmax、Topt),和最佳温度下的生长速率μopt。该模型是在经验基础上建立的作为描述数据的工具,模型的优点是所有参数都具有生理学意义,有利于对初始参数的估计。
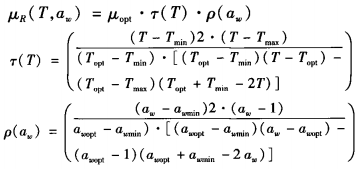
式中:μR为菌落径向生长速率;μopt菌落直径最大值;Tmin、Tmax、aopt)为菌株可以生长的最低和最高温度以及最小水分活度;Topt、aopt为菌落直径达到最大值时对应的温度和水分活度;awmax为1,方便计算无特殊意义。
声明:本文所用图片、文字来源《中国食品添加剂》,版权归原作者所有。如涉及作品内容、版权等问题,请与本网联系
相关链接:微生物,赭曲霉A,红曲霉